Durango Bill’s
Ramanujan Numbers
and
The Taxicab Problem
If you mention
the number “1729” or the phrase “Taxicab Problem” to any
mathematician, it will immediately bring up the subject of the
self-taught Indian mathematical genius Srinivasa Ramanujan.
When Ramanujan was dying of tuberculosis in a hospital, G. H.
Hardy would frequently visit him. It was on one of these
visits that the following occurred according to C. P. Snow.
Since then, integer solutions to:
I^3 + J^3 = K^3 + L^3
have been called “Ramanujan Numbers”.
The first five of these are:
Ramanujan Number
I J K L (No “,” With “,”)
----------------------------------------------
1 12 9 10 1729 1,729
2 16 9 15 4104 4,104
2 24 18 20 13832 13,832 (This is a multiple of Solution 1)
10 27 19 24 20683 20,683
4 32 18 30 32832 32,832 (This is a multiple of Solution 2)
The lowest solution to this “2-way” problem is also referred to as “Taxicab(2)”.
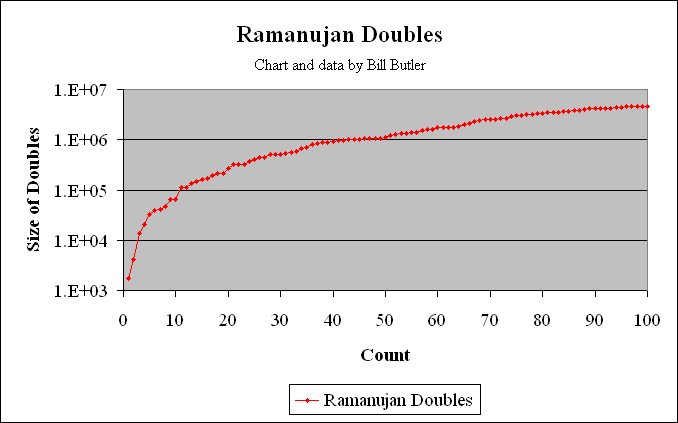
The graph above shows the distribution of the first 100 Ramanujan numbers (2-way pairs) in the number field. The 100th of these Ramanujan doubles occurs at: 64^3 + 164^3 = 25^3 + 167^3 = 4,673,088. Of these first 100 Ramanujan numbers, 49 are primitive as they are not multiples of smaller solutions. Multiples of all primitive solutions can be constructed by multiplying the I, J, K, L numbers above by 2, 3, 4, 5, etc.
Next, we might ask if there are any triple pair solutions to I^3 + J^3 = K^3 + L^3 = M^3 + N^3 where all the numbers are integers. Again, there are an infinite number of solutions. The first 5 solutions are:
Ramanujan Triple
I J K L M N (No “,” With “,”)
-----------------------------------------------------------------
228 423 167 436 255 414 87539319 87,539,319
11 493 90 492 346 428 119824488 119,824,488
111 522 408 423 359 460 143604279 143,604,279
70 560 198 552 315 525 175959000 175,959,000
339 661 300 670 510 580 327763000 327,763,000
Solutions involving 3 pairs are also called 3-way solutions. The lowest solution to any “N-Way” problem is also called a “Taxicab Number”. Thus “Taxicab(3)” is 87539319.
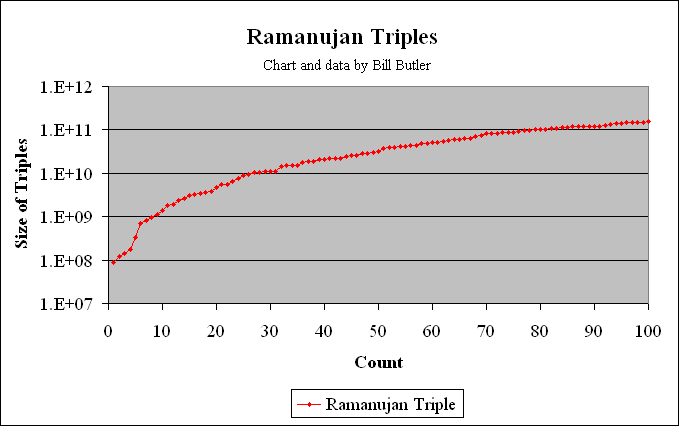
The graph above shows the magnitude of the first 100 of these Ramanujan triples. Of these one hundred 3-way solutions, 33 are primitive including all 5 of the above examples. The 100th of these “triples” is: 3806^3 + 4708^3 = 990^3 + 5412^3 = 121^3 + 5423^3 = 159,486,393,528. (Solution is not primitive.)
The sequence can be extended through Ramanujan Quadruples. (There are 4 ways that the sum of two cubes can share a common sum.) The first five quadruple pairs (I^3 + J^3 = K^3 + L^3 = M^3 + N^3 = O^3 + P^3) are:
Ramanujan
I J K L M N O P Quadruple
-----------------------------------------------------------------------
13322 16630 10200 18072 5436 18948 2421 19083 6,963,472,309,248
12939 21869 10362 22580 7068 23066 4275 23237 12,625,136,269,928
17176 25232 11772 26916 8664 27360 1539 27645 21,131,226,514,944
21930 24940 14577 28423 12900 28810 4170 29620 26,059,452,841,000
26644 33260 20400 36144 10872 37896 4842 38166 55,707,778,473,984 (A multiple)
Taxicab(4) is thus 6963472309248. The new version of the ramanujans.c program (see below) took 30 seconds to find Taxicab(4). (3GHz Pentium 4 running Windows XP) ) An early version of the rama4.c program ( earlier than http://www.durangobill.com/RamanujanPics/Rama4.html
- and even before the version at
http://web.archive.org/web/20020221182745/http://www.geocities.com/durangobill/Rama4.html ) running on an old 80386 computer actually found Taxicab(4) in 1987. (Never published.)
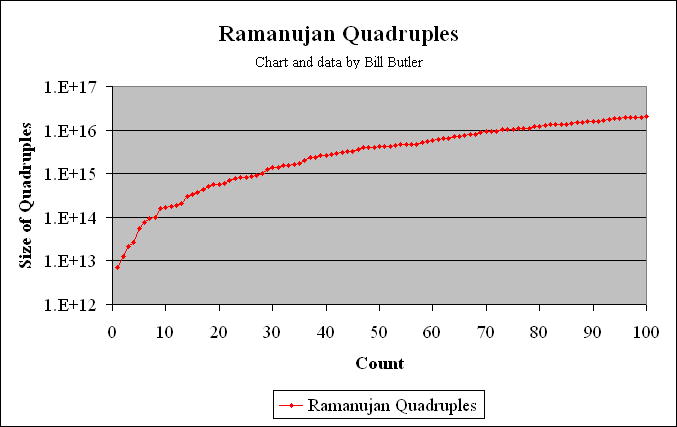
The graph above shows where the first 100 Ramanujan Quadruples appear in the number field. Total run time for all 100 solutions was 91 minutes. (Via the most recent optimized version of the ramanujans.c program on a 3GHz. Pentium 4.) If Taxicab(5) were plotted in the above graph, it would show up at position 143.
Of these one hundred 4-way solutions, there are 31 primitive solutions. The next 300 solutions add another 34 primitive solutions.
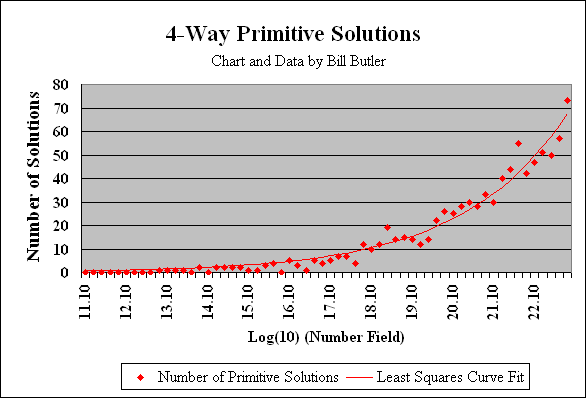
The graph above shows the distribution of the 867 primitive 4-way solutions within the number field out to 1.0E+23. The search for 4-way and higher solutions has confirmed other known Ramanujan results out through Taxicab(6).
The number field was segmented into standard geometric width ranges such that 5 consecutive ranges (as per tick marks) result in a factor-of-10 increase in the number field. The labels on the X axis show the log(10) of the location in the number field. For example, the “17.10” label represents the number field between 1.0E+17 and 1.585E+17. We note that log(10) of 1.0E+17 equals 17.0 and log(10) of 1.585E+17 equals 17.2. The 17.10 that is seen on the X axis is the midpoint of this range.
The plotted data points for each range are histogram counts of the number of primitive 4-way solutions within each range. For example, the data point at “Number of Solutions - 5” above the 17.10 label indicates there are five primitive 4-way solutions between 1.0E+17 and 1.585E+17.
The smooth line is a least squares exponential curve fit where A, B, C are least-squares calculated constants and X is Log(10) Number-field:
Y = A*exp((X-B)*C)
The least squares curve fit implies that the number of primitive 4-way solutions expands exponentially for every 10-fold increase in the number field. For example, the number of primitive 4-way solutions between 1.0E+19 and 1.0E+20 is about 47 % greater than the number of solutions between 1.0E+18 and 1.0E+19. Similarly, the number of primitive 4-way solutions between 1.0E+20 and 1.0E+21 expands by another ~47 %. There is no proof that this exponential curve accurately depicts what can be expected at still higher ranges, but it looks like it is an exponential function. Also, the number of primitive 5-way solutions looks like it follows a similar exponential function as you progress out into the number field. (See below)
Note: The “47 %” growth rate is a least squares calculation based on the most recent search results. If the search could be extended beyond 1.0E+23 changes in this calculated growth rate would be likely.
Also Note: Some primitive 4-way solutions have more than 1 combination of pairs to arrive at the same number. For example, in the first 5-way solution (below), the first 4 pairs form a primitive 4-way solution. If you instead use pairs 1, 2, 3, and 5, you have another set of 4 pairs that generates the same resultant number. When this happens, the result is only counted once for the above graphical tabulation of 4-way solutions.
Alternately, any 4 of the 5 pairs in any 5-way solution can be grouped to form a 4-way solution. If at least one of these groupings is primitive, then the result is counted as a primitive 4-way solution.
For example, in the third 5-way solution below, pairs 1, 2, 3, and 4 have a Greatest Common Divisor of 5 (hence, by themselves, are not primitive) while pairs 2, 3, 4 and 5 form a primitive 4-way solution. Thus the result is counted as a primitive 4-way solution as at least one grouping is primitive.
If you would like to see the 867 primitive 4-way solutions, please click here.
http://www.durangobill.com/RamanujanPics/Rama4way.html
If a number can be formed by the sum of 2 cubes in 5 different ways (5-way solution) it becomes a Ramanujan Quintuple. The first five 5-way solutions are shown in the table below. The lowest is of course “Taxicab(5)” which has been found/verified by several sources. The ramanujans.c program took 3 hrs. 15 min. for Taxicab(5). (The current optimized version cuts this to less than 2 hours.)
(I^3 + J^3 = K^3 + L^3 = M^3 + N^3 = O^3 + P^3 = Q^3 + R^3)
I J K L M N O P Q R
-------------------------------------------------------------------------------------
1) 231518 331954 221424 336588 205292 342952 107839 362753 38787 365757
2) 463036 663908 442848 673176 410584 685904 215678 725506 77574 731514
3) 579240 666630 543145 691295 285120 776070 233775 781785 48369 788631
4) 694554 995862 664272 1009764 615876 1028856 323517 1088259 116361 1097271
5) 926072 1327816 885696 1346352 821168 1371808 431356 1451012 155148 1463028
Equal:
(With “,”) (No “,”) Exponential
1) 48,988,659,276,962,496 48988659276962496 4.899E+16
2) 391,909,274,215,699,968 391909274215699968 3.919E+17
3) 490,593,422,681,271,000 490593422681271000 4.906E+17
4) 1,322,693,800,477,987,392 1322693800477987392 1.323E+18
5) 3,135,274,193,725,599,744 3135274193725599744 3.135E+18
Solutions 1 and 3 are primitive. Solutions 2, 4, and 5 are multiples of solution 1. The numbering system corresponds to data points in the graphs (below). The solution plots in the graphs consist of primitive solutions and assorted multiples. (Multiply the I, J, K, etc. by 2, 3, 4, etc.)
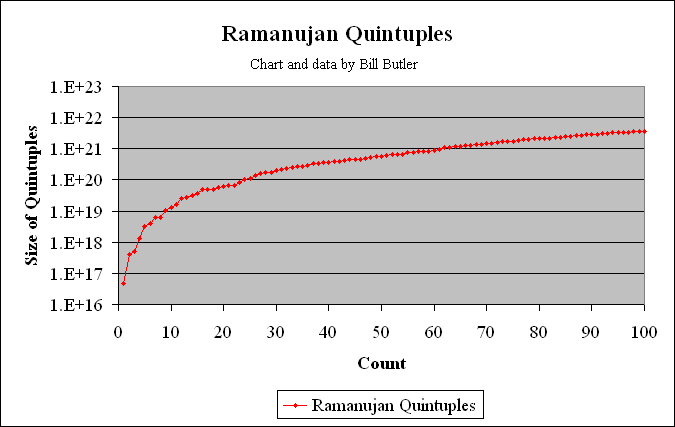
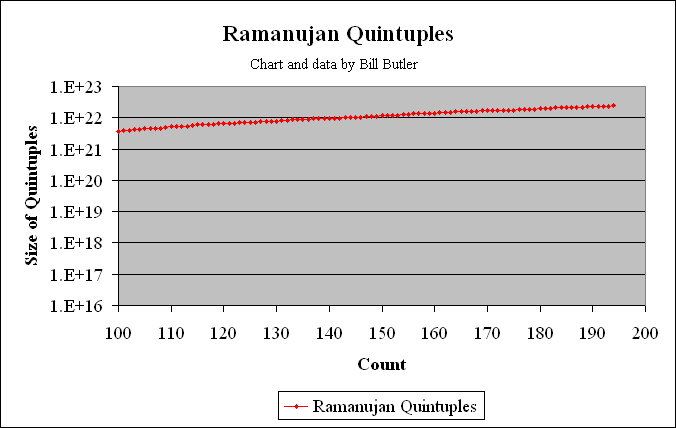
The two graphs above show all the 5-way solutions out through and including Taxicab(6) at position 194. There are a total of 193 5-way solutions less than Taxicab(6) which is the last plot. Data points consist of the 19 primitive 5-way solutions less than Taxicab(6), plus multiples thereof.
One possible way of constructing “N” way solutions is to start with “N-1” way (or lower) primitive solutions and generate all possible multiples to see if a higher order solution shows up. The graph below shows the result of these calculations.
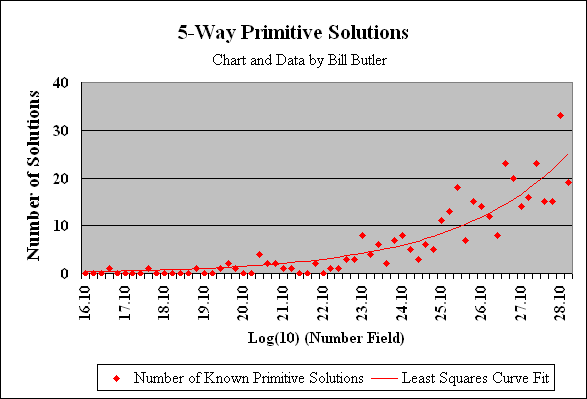
The graph above shows the distribution of known primitive 5-way solutions out to 2.51+E+28 (10^28.4). The plotting method is similar to what was used for the 4-way primitive solution graph.
Totals out to 1.0E+23 are complete while results out to 2.51+E+28 (10^28.4) have been calculated using known 4-way solutions. There may be additional solutions within this calculated number range.
If you would like to see the 357 known primitive 5-way solutions, please click here.
http://www.durangobill.com/RamanujanPics/Rama5way.html
The above results were found by a computer program written by the author. The source code for ramanujans.c may be viewed here. (http://www.durangobill.com/RamanujanPics/RamanujanC.html) It includes lots of documentation on how to calculate Ramanujan Numbers. The source code for the predecessor of this more recent version was rama4.c. (http://www.durangobill.com/RamanujanPics/Rama4.html) Users may use or modify either version without restriction or obligation. I would appreciate that any published results from modifications to either program include a note attributing the original algorithm to me. (The search used an optimized version of this program. While the optimized version more than doubled the execution speed, the posted version of the program gives a less cluttered picture of the algorithm.)
The ramanujans.c program will run as shown under Windows XP if compiled with the lcc-win32 “C” compiler. (http://www.cs.virginia.edu/~lcc-win32/
The process of “N-way” solutions can be extended to numbers that can be formed by the sum of 2 cubes in 6 different ways. There are several known solutions, and the lowest of these is shown below.
Taxicab(6) = 24153319581254312065344
= 28906206^3 + 582162^3
= 28894803^3 + 3064173^3
= 28657487^3 + 8519281^3
= 27093208^3 + 16218068^3
= 26590452^3 + 17492496^3
= 26224366^3 + 18289922^3
It is interesting to note that Taxicab(6) is 79 times Taxicab(5). If you multiply the I, J, K, etc. components of Taxicab(5) by 79, you will get the last 5 pairs of Taxicab(6). (The actual resulting number is 79^3 times larger.)
The previously mentioned method of using known 4-way solutions to generate higher order solutions was used to generate additional 6-way solutions out to the best known candidate for Taxicab(7). If you would like to see these 24 known primitive 6-way solutions, please click here.
http://www.durangobill.com/RamanujanPics/Rama6way.html
Use “Back” from your browser to return to this page.
Christian Boyer has extended the list of known primitive 6-way solutions and has published the best known candidate for Taxicab(7). (He also has candidates for higher order Taxicab numbers.) http://www.christianboyer.com/taxicab/
The author used the “multiples of 4-way solutions” algorithm (described earlier) out through this candidate for Taxicab(7). Based on the author’s results, it appears very highly probable that this candidate will in fact be eventually confirmed as Taxicab(7). This search also confirmed the earlier results by Christian Boyer.
1,847,282,122^ 3 + 2,648,660,966^3 =
1,766,742,096^3 + 2,685,635,652^3 =
1,638,024,868^3 + 2,736,414,008^3 =
860,447,381^3 + 2,894,406,187^3 =
459,531,128^3 + 2,915,734,948^3 =
309,481,473^3 + 2,918,375,103^3 =
58,798,362^3 + 2,919,526,806^3 =
24,885,189,317,885,898,975,235,988,544
Addition information on Ramanujan Numbers and the Taxicab Problem can be found at:
Christian Boyer’s web site: http://www.christianboyer.com/taxicab/ (Includes a photo of the real Taxicab 1729)
Also:
http://euler.free.fr/taxicab.htm
http://mathworld.wolfram.com/TaxicabNumber.html
Another variation of the Ramanujan/Taxicab problem involves sums of numbers where the numbers are raised to higher powers. For example: we may ask:
Are there any solutions to
I^4 + J^4 = K^4 + L^4 ?
It turns out that there are an infinite number of solutions, and there probably are an infinite number of primitive solutions. The first 5 solutions are:
1) 133^4 + 134^4 = 59^4 + 158^4 = 635,318,657 (Primitive)
2) 157^4 + 227^4 = 7^4 + 239^4 = 3,262,811,042 (Primitive)
3) 256^4 + 257^4 = 193^4 + 292^4 = 8,657,437,697 (Primitive)
4) 266^4 + 268^4 = 118^4 + 316^4 = 10,165,098,512 (A multiple of # 1)
5) 399^4 + 402^4 = 177^4 + 474^4 = 51,460,811,217 (A multiple of # 1)
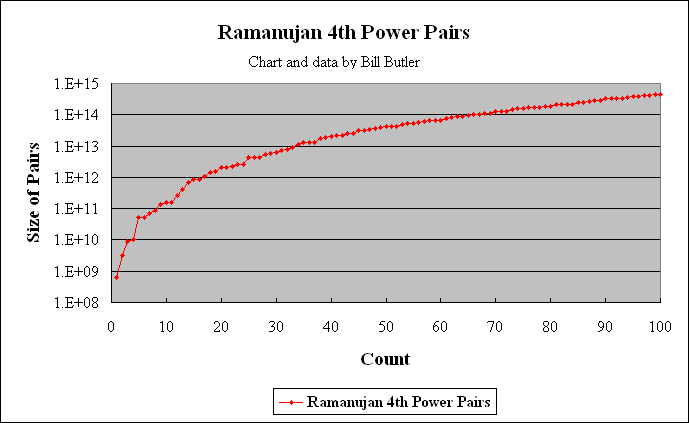
The graph above shows the distribution of the first 100 solutions to the problem I^4 + J^4 = K^4 + L^4. Of these 100 solutions, 15 are primitive (not a multiple of a lower solution) while 85 are multiples of lower solutions.
The search for primitive solutions was extended far beyond the previously known limit of 1.0E+24. Results are shown below.
Number of Cumulative
Number Primitive Primitive
Range Solutions Solutions
------------------------------------------------
1.0E8 to 1.0E9 1 1
1.0E9 to 1.0E10 2 3
1.0E10 to 1.0E11 2 5
1.0E11 to 1.0E12 1 6
1.0E12 to 1.0E13 2 8
1.0E13 to 1.0E14 4 12
1.0E14 to 1.0E15 6 18
1.0E15 to 1.0E16 15 33
1.0E16 to 1.0E17 22 55
1.0E17 to 1.0E18 15 70
1.0E18 to 1.0E19 25 95
1.0E19 to 1.0E20 48 143
1.0E20 to 1.0E21 58 201
1.0E21 to 1.0E22 68 269
1.0E22 to 1.0E23 98 367
1.0E23 to 1.0E24 148 515
1.0E24 to 1.0E25 150 665
1.0E25 to 1.0E26 184 849
1.0E26 to 1.0E27 252 1101
1.0E27 to 1.0E28 312 1413
Note: The above results extend far beyond previously known results. The I^4 + J^4 = K^4 + L^4 solutions can be seen here.
http://www.durangobill.com/RamanujanPics/Rama4thPower.html
The graph above shows the distribution of Ramanujan 4th power pairs out to 1.0E28. The format is similar to the previous 4-way and 5-way histogram charts. Again, each power-of-10 increase in the number field produces an exponential (or near exponential) increase in the number of solutions. The least squares exponential curve fit indicates that each power of ten increase in the number field produces about a 28 % increase in the number of solutions per log(10) range of numbers.
The next question that we might ask is:
Are there any triple pair solutions to
I^4 + J^4 = K^4 + L^4 = M^4 + N^4 ?
The answer is not known. The search was run to 1.0E+28 without finding a solution. It’s possible the computer program was faulty. It’s possible that a solution exists out beyond 1.0E28. At this point all we can say is that no solutions are known.
A search was also carried out for 5th power solutions. For example:
Are there any solutions to I^5 + J^5 = K^5 + L^5 ?
A search was made out to 3.6E+28 for fifth power solutions. No solutions were found. Again it might be that the computer program was faulty, or solutions might exist above 3.6E+28. The computer program that was used was essentially the same as the posted ramanujans.c program that was referenced earlier - except the cubes tables were replaced by fifth powers. For the fifth power search, regular “double” variables were replaced by “long double”. The extra precision allowed the search to run to 3.6E+28.
A similar search was run for sixth power solutions out to 3.6E+28. (e.g. I^6 + J^6 = K^6 + L^6) Nothing was found here either.
While “Taxicab(N)” is defined as the lowest number that can be formed by the sum of two cubes in “N” different ways, Cabtaxi(N) is defined as the lowest number that can be formed by the sum and/or difference of two cubes in “N” different ways. (See http://en.wikipedia.org/wiki/Cabtaxi_number for more information.)
Cabtaxi(1) through Cabtaxi(9) were previously known. The author ran a search via the Cabtaxi.c program ( http://www.durangobill.com/RamanujanPics/CabtaxiC.html ) which confirmed the results shown below.
Cabtaxi(1) = 1
= 1^3 + 0^3
Cabtaxi(2) = 91
= 3^3 + 4^3
= 6^3 - 5^3
Cabtaxi(3) = 728
= 6^3 + 8^3
= 9^3 - 1^3
= 12^3 - 10^3
Cabtaxi(4) = 2,741,256
= 108^3 + 114^3
= 140^3 - 14^3
= 168^3 - 126^3
= 207^3 - 183^3
Cabtaxi(5) = 6,017,193
= 166^3 + 113^3
= 180^3 + 57^3
= 185^3 - 68^3
= 209^3 - 146^3
= 246^3 - 207^3
Cabtaxi(6) = 1,412,774,811
= 963^3 + 804^3
= 1,134^3 - 357^3
= 1,155^3 - 504^3
= 1,246^3 - 805^3
= 2,115^3 - 2,004^3
= 4,746^3 - 4,725^3
Cabtaxi(7) = 11,302,198,488
= 1,926^3 + 1,608^3
= 1,939^3 + 1,589^3
= 2,268^3 - 714^3
= 2,310^3 - 1,008^3
= 2,492^3 - 1,610^3
= 4,230^3 - 4,008^3
= 9,492^3 - 9,450^3
Cabtaxi(8) = 137,513,849,003,496
= 22,944^3 + 50,058^3
= 36,547^3 + 44,597^3
= 36,984^3 + 44,298^3
= 52,164^3 - 16,422^3
= 53,130^3 - 23,184^3
= 57,316^3 - 37,030^3
= 97,290^3 - 92,184^3
= 218,316^3 - 217,350^3
Cabtaxi(9) = 424,910,390,480,793,000
= 645,210^3 + 538,680^3
= 649,565^3 + 532,315^3
= 752,409^3 - 101,409^3
= 759,780^3 - 239,190^3
= 773,850^3 - 337,680^3
= 834,820^3 - 539,350^3
= 1,417,050^3 - 1,342,680^3
= 3,179,820^3 - 3,165,750^3
= 5,960,010^3 - 5,956,020^3
Cabtaxi(10) has been confirmed by the author’s computer program and is equal to:
933,528,127,886,302,221,000
= 7,002,840^3 + 8,387,730^3
= 6,920,095^3 + 8,444,345^3
= 77,480,130^3 - 77,428,260^3
= 41,337,660^3 - 41,154,750^3
= 18,421,650^3 - 17,454,840^3
= 10,852,660^3 - 7,011,550^3
= 10,060,050^3 - 4,389,840^3
= 9,877,140^3 - 3,109,470^3
= 9,781,317^3 - 1,318,317^3
= 9,773,330^3 - 84,560^3
Christian Boyer had previously calculated a list of primitive 9-way solutions less than his candidate for Cabtaxi(10).
http://www.christianboyer.com/taxicab
http://www.christianboyer.com/taxicab/ListCabtaxi9_10.txt
(As displayed on the above web page)
# Ways Number
1 9 424910390480793000
2 9 825001442051661504
3 9 1153657786768695936
4 9 6123582409620312000
5 9 7468225023090417768
6 9 7545659922519832512
7 9 10933313592720956472
8 9 24326499458358849024
9 9 41359077767838467448
10 9 45307115612467444008
11 9 49308192936614146752
12 9 186525463571696587968
13 9 270266803327651272408
14 9 272257988363832744000
15 9 293071805905425386112
16 9 346083762520724574528
17 9 445079976262957683648
18 9 572219233725765415608
19 9 842751835937888190552
20 10 933528127886302221000
The program confirmed that Christian’s list of primitive 9-way solutions is in fact complete, and that his candidate for Cabtaxi(10) is in fact the lowest primitive 10-way solution.
The source code for the author’s Cabtaxi computer program is at http://www.durangobill.com/RamanujanPics/CabtaxiC.html - lots of documentation. (The Skulltrail computer ran multiple copies using a slightly different version.) The program will run as is without modification if compiled with the lcc-win32 “C” compiler. http://www.cs.virginia.edu/~lcc-win32/ )
Addition information on Ramanujan Numbers and the Taxicab Problem can be found at:
Christian Boyer’s web site http://www.christianboyer.com/taxicab/ (Includes a photo of the real Taxicab 1729)
http://euler.free.fr/taxicab.htm
http://mathworld.wolfram.com/TaxicabNumber.html
Return to Durango Bill's Home Page
Web page generated via Sea Monkey's Composer HTML editor
within a Linux Cinnamon Mint 18 operating system.
(Goodbye Microsoft)
“Hardy used to
visit him, as he lay dying in hospital at Putney. It was on
one of those visits that there happened the incident of the
taxicab number. Hardy had gone out to Putney by taxi, as
usual his chosen method of conveyance. He went into the room
where Ramanujan was lying. Hardy, always inept about
introducing a conversation, said, probably without a
greeting, and certainly as his first remark: ‘I thought the
number of my taxicab was 1729. It seemed to me rather a dull
number.’ To which Ramanujan replied: ‘No, Hardy! No, Hardy!
It is a very interesting number. It is the smallest number
expressible as the sum of two cubes in two different ways.’”
Since then, integer solutions to:
I^3 + J^3 = K^3 + L^3
have been called “Ramanujan Numbers”.
The first five of these are:
Ramanujan Number
I J K L (No “,” With “,”)
----------------------------------------------
1 12 9 10 1729 1,729
2 16 9 15 4104 4,104
2 24 18 20 13832 13,832 (This is a multiple of Solution 1)
10 27 19 24 20683 20,683
4 32 18 30 32832 32,832 (This is a multiple of Solution 2)
The lowest solution to this “2-way” problem is also referred to as “Taxicab(2)”.

The graph above shows the distribution of the first 100 Ramanujan numbers (2-way pairs) in the number field. The 100th of these Ramanujan doubles occurs at: 64^3 + 164^3 = 25^3 + 167^3 = 4,673,088. Of these first 100 Ramanujan numbers, 49 are primitive as they are not multiples of smaller solutions. Multiples of all primitive solutions can be constructed by multiplying the I, J, K, L numbers above by 2, 3, 4, 5, etc.
Ramanujan
Triples
Next, we might ask if there are any triple pair solutions to I^3 + J^3 = K^3 + L^3 = M^3 + N^3 where all the numbers are integers. Again, there are an infinite number of solutions. The first 5 solutions are:
Ramanujan Triple
I J K L M N (No “,” With “,”)
-----------------------------------------------------------------
228 423 167 436 255 414 87539319 87,539,319
11 493 90 492 346 428 119824488 119,824,488
111 522 408 423 359 460 143604279 143,604,279
70 560 198 552 315 525 175959000 175,959,000
339 661 300 670 510 580 327763000 327,763,000
Solutions involving 3 pairs are also called 3-way solutions. The lowest solution to any “N-Way” problem is also called a “Taxicab Number”. Thus “Taxicab(3)” is 87539319.

The graph above shows the magnitude of the first 100 of these Ramanujan triples. Of these one hundred 3-way solutions, 33 are primitive including all 5 of the above examples. The 100th of these “triples” is: 3806^3 + 4708^3 = 990^3 + 5412^3 = 121^3 + 5423^3 = 159,486,393,528. (Solution is not primitive.)
Ramanujan
Quadruples
The sequence can be extended through Ramanujan Quadruples. (There are 4 ways that the sum of two cubes can share a common sum.) The first five quadruple pairs (I^3 + J^3 = K^3 + L^3 = M^3 + N^3 = O^3 + P^3) are:
Ramanujan
I J K L M N O P Quadruple
-----------------------------------------------------------------------
13322 16630 10200 18072 5436 18948 2421 19083 6,963,472,309,248
12939 21869 10362 22580 7068 23066 4275 23237 12,625,136,269,928
17176 25232 11772 26916 8664 27360 1539 27645 21,131,226,514,944
21930 24940 14577 28423 12900 28810 4170 29620 26,059,452,841,000
26644 33260 20400 36144 10872 37896 4842 38166 55,707,778,473,984 (A multiple)
Taxicab(4) is thus 6963472309248. The new version of the ramanujans.c program (see below) took 30 seconds to find Taxicab(4). (3GHz Pentium 4 running Windows XP) ) An early version of the rama4.c program ( earlier than http://www.durangobill.com/RamanujanPics/Rama4.html
- and even before the version at
http://web.archive.org/web/20020221182745/http://www.geocities.com/durangobill/Rama4.html ) running on an old 80386 computer actually found Taxicab(4) in 1987. (Never published.)

The graph above shows where the first 100 Ramanujan Quadruples appear in the number field. Total run time for all 100 solutions was 91 minutes. (Via the most recent optimized version of the ramanujans.c program on a 3GHz. Pentium 4.) If Taxicab(5) were plotted in the above graph, it would show up at position 143.
Of these one hundred 4-way solutions, there are 31 primitive solutions. The next 300 solutions add another 34 primitive solutions.

The graph above shows the distribution of the 867 primitive 4-way solutions within the number field out to 1.0E+23. The search for 4-way and higher solutions has confirmed other known Ramanujan results out through Taxicab(6).
The number field was segmented into standard geometric width ranges such that 5 consecutive ranges (as per tick marks) result in a factor-of-10 increase in the number field. The labels on the X axis show the log(10) of the location in the number field. For example, the “17.10” label represents the number field between 1.0E+17 and 1.585E+17. We note that log(10) of 1.0E+17 equals 17.0 and log(10) of 1.585E+17 equals 17.2. The 17.10 that is seen on the X axis is the midpoint of this range.
The plotted data points for each range are histogram counts of the number of primitive 4-way solutions within each range. For example, the data point at “Number of Solutions - 5” above the 17.10 label indicates there are five primitive 4-way solutions between 1.0E+17 and 1.585E+17.
The smooth line is a least squares exponential curve fit where A, B, C are least-squares calculated constants and X is Log(10) Number-field:
Y = A*exp((X-B)*C)
The least squares curve fit implies that the number of primitive 4-way solutions expands exponentially for every 10-fold increase in the number field. For example, the number of primitive 4-way solutions between 1.0E+19 and 1.0E+20 is about 47 % greater than the number of solutions between 1.0E+18 and 1.0E+19. Similarly, the number of primitive 4-way solutions between 1.0E+20 and 1.0E+21 expands by another ~47 %. There is no proof that this exponential curve accurately depicts what can be expected at still higher ranges, but it looks like it is an exponential function. Also, the number of primitive 5-way solutions looks like it follows a similar exponential function as you progress out into the number field. (See below)
Note: The “47 %” growth rate is a least squares calculation based on the most recent search results. If the search could be extended beyond 1.0E+23 changes in this calculated growth rate would be likely.
Also Note: Some primitive 4-way solutions have more than 1 combination of pairs to arrive at the same number. For example, in the first 5-way solution (below), the first 4 pairs form a primitive 4-way solution. If you instead use pairs 1, 2, 3, and 5, you have another set of 4 pairs that generates the same resultant number. When this happens, the result is only counted once for the above graphical tabulation of 4-way solutions.
Alternately, any 4 of the 5 pairs in any 5-way solution can be grouped to form a 4-way solution. If at least one of these groupings is primitive, then the result is counted as a primitive 4-way solution.
For example, in the third 5-way solution below, pairs 1, 2, 3, and 4 have a Greatest Common Divisor of 5 (hence, by themselves, are not primitive) while pairs 2, 3, 4 and 5 form a primitive 4-way solution. Thus the result is counted as a primitive 4-way solution as at least one grouping is primitive.
If you would like to see the 867 primitive 4-way solutions, please click here.
http://www.durangobill.com/RamanujanPics/Rama4way.html
Ramanujan
Quintuples
If a number can be formed by the sum of 2 cubes in 5 different ways (5-way solution) it becomes a Ramanujan Quintuple. The first five 5-way solutions are shown in the table below. The lowest is of course “Taxicab(5)” which has been found/verified by several sources. The ramanujans.c program took 3 hrs. 15 min. for Taxicab(5). (The current optimized version cuts this to less than 2 hours.)
(I^3 + J^3 = K^3 + L^3 = M^3 + N^3 = O^3 + P^3 = Q^3 + R^3)
I J K L M N O P Q R
-------------------------------------------------------------------------------------
1) 231518 331954 221424 336588 205292 342952 107839 362753 38787 365757
2) 463036 663908 442848 673176 410584 685904 215678 725506 77574 731514
3) 579240 666630 543145 691295 285120 776070 233775 781785 48369 788631
4) 694554 995862 664272 1009764 615876 1028856 323517 1088259 116361 1097271
5) 926072 1327816 885696 1346352 821168 1371808 431356 1451012 155148 1463028
Equal:
(With “,”) (No “,”) Exponential
1) 48,988,659,276,962,496 48988659276962496 4.899E+16
2) 391,909,274,215,699,968 391909274215699968 3.919E+17
3) 490,593,422,681,271,000 490593422681271000 4.906E+17
4) 1,322,693,800,477,987,392 1322693800477987392 1.323E+18
5) 3,135,274,193,725,599,744 3135274193725599744 3.135E+18
Solutions 1 and 3 are primitive. Solutions 2, 4, and 5 are multiples of solution 1. The numbering system corresponds to data points in the graphs (below). The solution plots in the graphs consist of primitive solutions and assorted multiples. (Multiply the I, J, K, etc. by 2, 3, 4, etc.)


The two graphs above show all the 5-way solutions out through and including Taxicab(6) at position 194. There are a total of 193 5-way solutions less than Taxicab(6) which is the last plot. Data points consist of the 19 primitive 5-way solutions less than Taxicab(6), plus multiples thereof.
One possible way of constructing “N” way solutions is to start with “N-1” way (or lower) primitive solutions and generate all possible multiples to see if a higher order solution shows up. The graph below shows the result of these calculations.

The graph above shows the distribution of known primitive 5-way solutions out to 2.51+E+28 (10^28.4). The plotting method is similar to what was used for the 4-way primitive solution graph.
Totals out to 1.0E+23 are complete while results out to 2.51+E+28 (10^28.4) have been calculated using known 4-way solutions. There may be additional solutions within this calculated number range.
If you would like to see the 357 known primitive 5-way solutions, please click here.
http://www.durangobill.com/RamanujanPics/Rama5way.html
The above results were found by a computer program written by the author. The source code for ramanujans.c may be viewed here. (http://www.durangobill.com/RamanujanPics/RamanujanC.html) It includes lots of documentation on how to calculate Ramanujan Numbers. The source code for the predecessor of this more recent version was rama4.c. (http://www.durangobill.com/RamanujanPics/Rama4.html) Users may use or modify either version without restriction or obligation. I would appreciate that any published results from modifications to either program include a note attributing the original algorithm to me. (The search used an optimized version of this program. While the optimized version more than doubled the execution speed, the posted version of the program gives a less cluttered picture of the algorithm.)
The ramanujans.c program will run as shown under Windows XP if compiled with the lcc-win32 “C” compiler. (http://www.cs.virginia.edu/~lcc-win32/
Ramanujan
Sextuples
The process of “N-way” solutions can be extended to numbers that can be formed by the sum of 2 cubes in 6 different ways. There are several known solutions, and the lowest of these is shown below.
Taxicab(6) = 24153319581254312065344
= 28906206^3 + 582162^3
= 28894803^3 + 3064173^3
= 28657487^3 + 8519281^3
= 27093208^3 + 16218068^3
= 26590452^3 + 17492496^3
= 26224366^3 + 18289922^3
It is interesting to note that Taxicab(6) is 79 times Taxicab(5). If you multiply the I, J, K, etc. components of Taxicab(5) by 79, you will get the last 5 pairs of Taxicab(6). (The actual resulting number is 79^3 times larger.)
The previously mentioned method of using known 4-way solutions to generate higher order solutions was used to generate additional 6-way solutions out to the best known candidate for Taxicab(7). If you would like to see these 24 known primitive 6-way solutions, please click here.
http://www.durangobill.com/RamanujanPics/Rama6way.html
Use “Back” from your browser to return to this page.
Ramanujan
Septuples - Taxicab(7)
Christian Boyer has extended the list of known primitive 6-way solutions and has published the best known candidate for Taxicab(7). (He also has candidates for higher order Taxicab numbers.) http://www.christianboyer.com/taxicab/
The author used the “multiples of 4-way solutions” algorithm (described earlier) out through this candidate for Taxicab(7). Based on the author’s results, it appears very highly probable that this candidate will in fact be eventually confirmed as Taxicab(7). This search also confirmed the earlier results by Christian Boyer.
1,847,282,122^ 3 + 2,648,660,966^3 =
1,766,742,096^3 + 2,685,635,652^3 =
1,638,024,868^3 + 2,736,414,008^3 =
860,447,381^3 + 2,894,406,187^3 =
459,531,128^3 + 2,915,734,948^3 =
309,481,473^3 + 2,918,375,103^3 =
58,798,362^3 + 2,919,526,806^3 =
24,885,189,317,885,898,975,235,988,544
Addition information on Ramanujan Numbers and the Taxicab Problem can be found at:
Christian Boyer’s web site: http://www.christianboyer.com/taxicab/ (Includes a photo of the real Taxicab 1729)
Also:
http://euler.free.fr/taxicab.htm
http://mathworld.wolfram.com/TaxicabNumber.html
Solutions
involving Higher Powers
Another variation of the Ramanujan/Taxicab problem involves sums of numbers where the numbers are raised to higher powers. For example: we may ask:
Are there any solutions to
I^4 + J^4 = K^4 + L^4 ?
It turns out that there are an infinite number of solutions, and there probably are an infinite number of primitive solutions. The first 5 solutions are:
1) 133^4 + 134^4 = 59^4 + 158^4 = 635,318,657 (Primitive)
2) 157^4 + 227^4 = 7^4 + 239^4 = 3,262,811,042 (Primitive)
3) 256^4 + 257^4 = 193^4 + 292^4 = 8,657,437,697 (Primitive)
4) 266^4 + 268^4 = 118^4 + 316^4 = 10,165,098,512 (A multiple of # 1)
5) 399^4 + 402^4 = 177^4 + 474^4 = 51,460,811,217 (A multiple of # 1)

The graph above shows the distribution of the first 100 solutions to the problem I^4 + J^4 = K^4 + L^4. Of these 100 solutions, 15 are primitive (not a multiple of a lower solution) while 85 are multiples of lower solutions.
The search for primitive solutions was extended far beyond the previously known limit of 1.0E+24. Results are shown below.
Number of Cumulative
Number Primitive Primitive
Range Solutions Solutions
------------------------------------------------
1.0E8 to 1.0E9 1 1
1.0E9 to 1.0E10 2 3
1.0E10 to 1.0E11 2 5
1.0E11 to 1.0E12 1 6
1.0E12 to 1.0E13 2 8
1.0E13 to 1.0E14 4 12
1.0E14 to 1.0E15 6 18
1.0E15 to 1.0E16 15 33
1.0E16 to 1.0E17 22 55
1.0E17 to 1.0E18 15 70
1.0E18 to 1.0E19 25 95
1.0E19 to 1.0E20 48 143
1.0E20 to 1.0E21 58 201
1.0E21 to 1.0E22 68 269
1.0E22 to 1.0E23 98 367
1.0E23 to 1.0E24 148 515
1.0E24 to 1.0E25 150 665
1.0E25 to 1.0E26 184 849
1.0E26 to 1.0E27 252 1101
1.0E27 to 1.0E28 312 1413
Note: The above results extend far beyond previously known results. The I^4 + J^4 = K^4 + L^4 solutions can be seen here.
http://www.durangobill.com/RamanujanPics/Rama4thPower.html

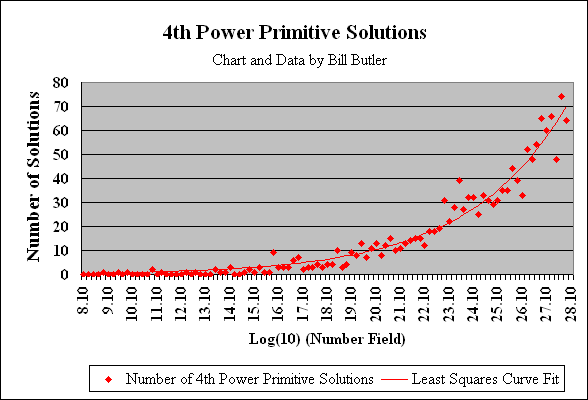
The graph above shows the distribution of Ramanujan 4th power pairs out to 1.0E28. The format is similar to the previous 4-way and 5-way histogram charts. Again, each power-of-10 increase in the number field produces an exponential (or near exponential) increase in the number of solutions. The least squares exponential curve fit indicates that each power of ten increase in the number field produces about a 28 % increase in the number of solutions per log(10) range of numbers.
The next question that we might ask is:
Are there any triple pair solutions to
I^4 + J^4 = K^4 + L^4 = M^4 + N^4 ?
The answer is not known. The search was run to 1.0E+28 without finding a solution. It’s possible the computer program was faulty. It’s possible that a solution exists out beyond 1.0E28. At this point all we can say is that no solutions are known.
A search was also carried out for 5th power solutions. For example:
Are there any solutions to I^5 + J^5 = K^5 + L^5 ?
A search was made out to 3.6E+28 for fifth power solutions. No solutions were found. Again it might be that the computer program was faulty, or solutions might exist above 3.6E+28. The computer program that was used was essentially the same as the posted ramanujans.c program that was referenced earlier - except the cubes tables were replaced by fifth powers. For the fifth power search, regular “double” variables were replaced by “long double”. The extra precision allowed the search to run to 3.6E+28.
A similar search was run for sixth power solutions out to 3.6E+28. (e.g. I^6 + J^6 = K^6 + L^6) Nothing was found here either.
Cabtaxi
Numbers
While “Taxicab(N)” is defined as the lowest number that can be formed by the sum of two cubes in “N” different ways, Cabtaxi(N) is defined as the lowest number that can be formed by the sum and/or difference of two cubes in “N” different ways. (See http://en.wikipedia.org/wiki/Cabtaxi_number for more information.)
Cabtaxi(1) through Cabtaxi(9) were previously known. The author ran a search via the Cabtaxi.c program ( http://www.durangobill.com/RamanujanPics/CabtaxiC.html ) which confirmed the results shown below.
Cabtaxi(1) = 1
= 1^3 + 0^3
Cabtaxi(2) = 91
= 3^3 + 4^3
= 6^3 - 5^3
Cabtaxi(3) = 728
= 6^3 + 8^3
= 9^3 - 1^3
= 12^3 - 10^3
Cabtaxi(4) = 2,741,256
= 108^3 + 114^3
= 140^3 - 14^3
= 168^3 - 126^3
= 207^3 - 183^3
Cabtaxi(5) = 6,017,193
= 166^3 + 113^3
= 180^3 + 57^3
= 185^3 - 68^3
= 209^3 - 146^3
= 246^3 - 207^3
Cabtaxi(6) = 1,412,774,811
= 963^3 + 804^3
= 1,134^3 - 357^3
= 1,155^3 - 504^3
= 1,246^3 - 805^3
= 2,115^3 - 2,004^3
= 4,746^3 - 4,725^3
Cabtaxi(7) = 11,302,198,488
= 1,926^3 + 1,608^3
= 1,939^3 + 1,589^3
= 2,268^3 - 714^3
= 2,310^3 - 1,008^3
= 2,492^3 - 1,610^3
= 4,230^3 - 4,008^3
= 9,492^3 - 9,450^3
Cabtaxi(8) = 137,513,849,003,496
= 22,944^3 + 50,058^3
= 36,547^3 + 44,597^3
= 36,984^3 + 44,298^3
= 52,164^3 - 16,422^3
= 53,130^3 - 23,184^3
= 57,316^3 - 37,030^3
= 97,290^3 - 92,184^3
= 218,316^3 - 217,350^3
Cabtaxi(9) = 424,910,390,480,793,000
= 645,210^3 + 538,680^3
= 649,565^3 + 532,315^3
= 752,409^3 - 101,409^3
= 759,780^3 - 239,190^3
= 773,850^3 - 337,680^3
= 834,820^3 - 539,350^3
= 1,417,050^3 - 1,342,680^3
= 3,179,820^3 - 3,165,750^3
= 5,960,010^3 - 5,956,020^3
Cabtaxi(10) has been confirmed by the author’s computer program and is equal to:
933,528,127,886,302,221,000
= 7,002,840^3 + 8,387,730^3
= 6,920,095^3 + 8,444,345^3
= 77,480,130^3 - 77,428,260^3
= 41,337,660^3 - 41,154,750^3
= 18,421,650^3 - 17,454,840^3
= 10,852,660^3 - 7,011,550^3
= 10,060,050^3 - 4,389,840^3
= 9,877,140^3 - 3,109,470^3
= 9,781,317^3 - 1,318,317^3
= 9,773,330^3 - 84,560^3
Christian Boyer had previously calculated a list of primitive 9-way solutions less than his candidate for Cabtaxi(10).
http://www.christianboyer.com/taxicab
http://www.christianboyer.com/taxicab/ListCabtaxi9_10.txt
(As displayed on the above web page)
# Ways Number
1 9 424910390480793000
2 9 825001442051661504
3 9 1153657786768695936
4 9 6123582409620312000
5 9 7468225023090417768
6 9 7545659922519832512
7 9 10933313592720956472
8 9 24326499458358849024
9 9 41359077767838467448
10 9 45307115612467444008
11 9 49308192936614146752
12 9 186525463571696587968
13 9 270266803327651272408
14 9 272257988363832744000
15 9 293071805905425386112
16 9 346083762520724574528
17 9 445079976262957683648
18 9 572219233725765415608
19 9 842751835937888190552
20 10 933528127886302221000
The program confirmed that Christian’s list of primitive 9-way solutions is in fact complete, and that his candidate for Cabtaxi(10) is in fact the lowest primitive 10-way solution.
The source code for the author’s Cabtaxi computer program is at http://www.durangobill.com/RamanujanPics/CabtaxiC.html - lots of documentation. (The Skulltrail computer ran multiple copies using a slightly different version.) The program will run as is without modification if compiled with the lcc-win32 “C” compiler. http://www.cs.virginia.edu/~lcc-win32/ )
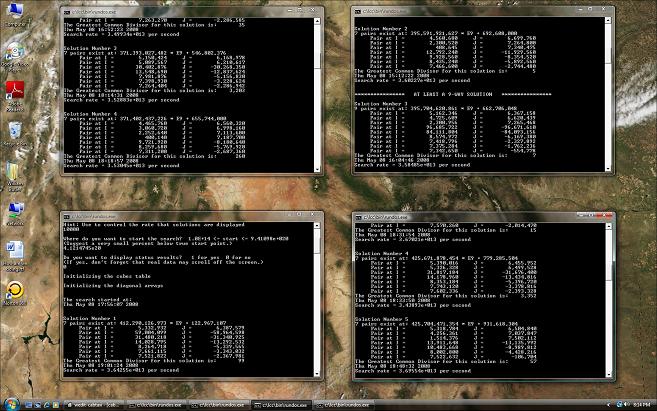
(Click on the above small
image to see a full size image which shows)
(4 copies of the CabtaxiC program working on the Cabtaxi problem.)
The picture above shows interim Cabtaxi search results as of May 8, 2008.
(4 copies of the CabtaxiC program working on the Cabtaxi problem.)
The picture above shows interim Cabtaxi search results as of May 8, 2008.
Addition information on Ramanujan Numbers and the Taxicab Problem can be found at:
Christian Boyer’s web site http://www.christianboyer.com/taxicab/ (Includes a photo of the real Taxicab 1729)
http://euler.free.fr/taxicab.htm
http://mathworld.wolfram.com/TaxicabNumber.html
Return to Durango Bill's Home Page
Web page generated via Sea Monkey's Composer HTML editor
within a Linux Cinnamon Mint 18 operating system.
(Goodbye Microsoft)