Durango Bill’s
Epitrochoids and Hypotrochoids
Epitrochoids and Hypotrochoids are members of the Trochoid
family. They are formed by rolling one circle around another stationary
circle, and the specific curve is formed by the path generated by the
end of an arm which is fixed to the rolling circle. A limited number of
these curves can be generated by the commercially sold Spirograph game,
but mathematically, the possibilities are much richer.
We will first look at an example of an Epitrochoid which
is formed by rolling one circle around the outside of another circle.
Further down this page we will look at Hypotrochoids which are formed
by rolling one circle around the inside of another. All graphs on this
page were generated via Microsoft’s Excel.
Epitrochoids
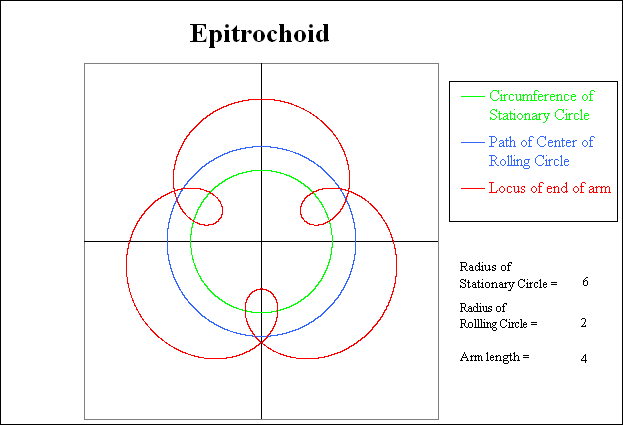
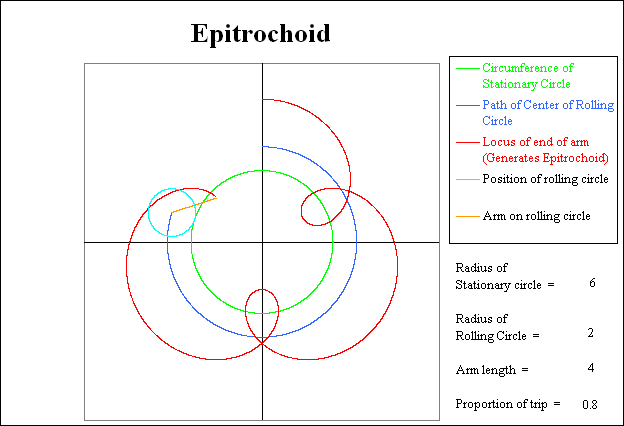
The graph below shows an Epitrochoid that is formed when a
small circle with a radius of 2 is rolled around the outside of a
circle with a radius of 6. An arm with a length of 4 has one end
attached to the center of the rolling circle. The path of the other end
of the arm is shown in red and forms the Epitrochoid. The circumference
of the stationary circle is shown in green while the path taken by the
center of the rolling circle is shown in dark blue.
The following sequence of pictures show various stages in
the generation of the Epitrochoid. In each picture, the circumference
of the stationary circle is shown in green. The current position of the
rolling circle is shown in light blue. The trace of the path taken by
the center of the rolling circle is shown in dark blue. The current
position of the arm attached to the rolling circle is shown in orange.
Finally the path generated by the outer end of the arm generates the
Epitrochoid, and is shown in red.
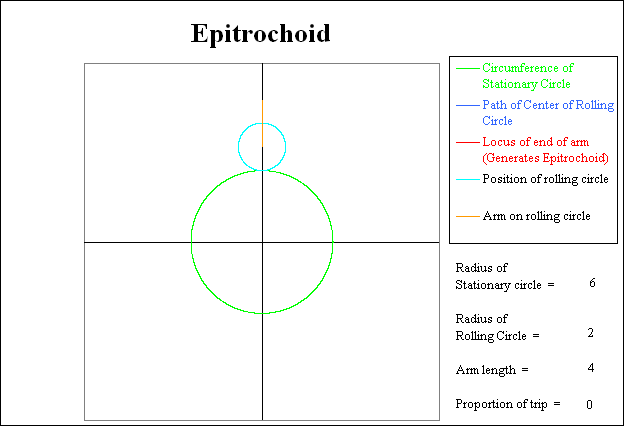
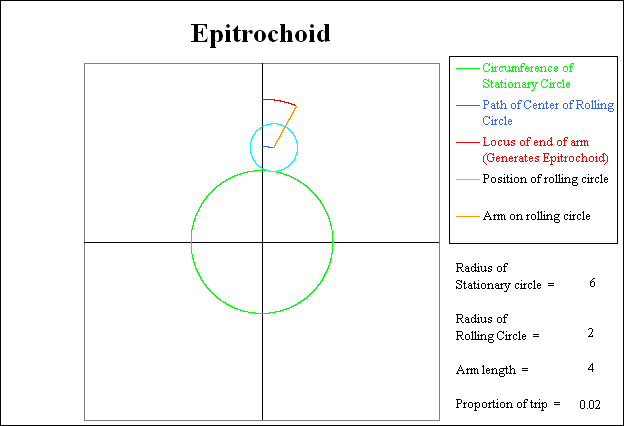
Initially the rolling circle starts at the top of the
stationary circle. The orange arm is straight up and overlies part of
the Y axis. There is no red or dark blue line yet as nothing has moved.
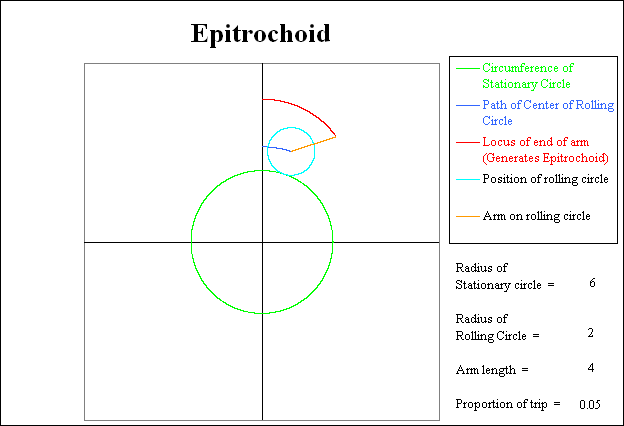
Here, the rolling circle has started its clockwise trip
around the stationary circle. The dark blue line shows the path of the
center of the rolling circle while the outer end of the arm is
beginning to generate the Epitrochoid. At this stage the rolling circle
has completed 2 % of its trip.
The following sequence of pictures show subsequent stages
in the formation of the Epitrochoid. The legend in the lower right
portion of each picture displays the relative progress.
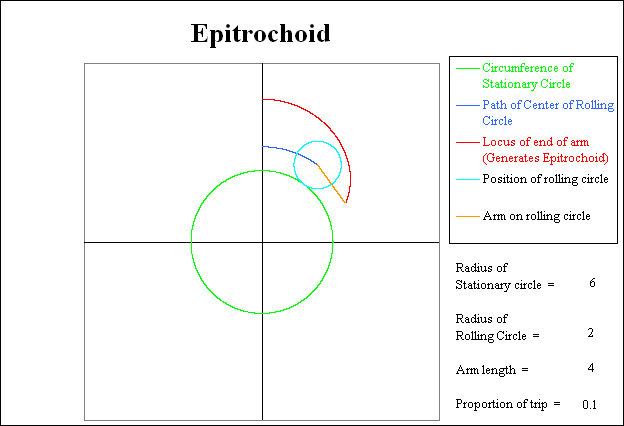
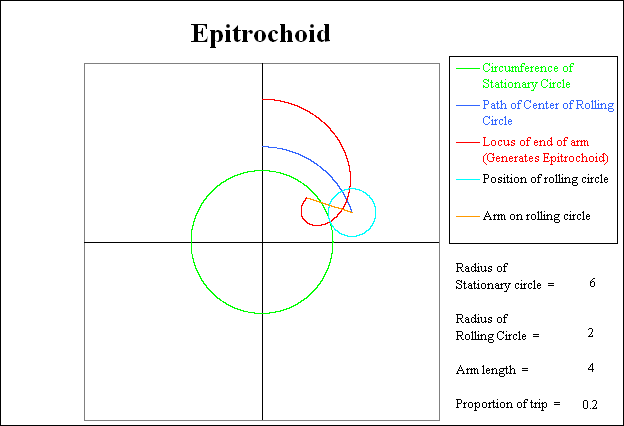
The radius of the stationary green inner circle is 6. The
radius of the light blue, rolling circle is 2. Thus the rolling circle
will rotate 6 / 2 = 3 times relative to the stationary circle while it
is rolling around the stationary circle. Since the clockwise direction
that the rolling circle is moving produces a clockwise relative
rotation of the arm, the total number of revolutions of the arm
relative to the coordinate system will be 3 + 1 = 4. The arm will be
straight up at trip proportion locations of 0.25, 0.50, 0.75, and 1.00.
When the earth rotates around the sun a similar rotation
phenomenon exists. The earth rotates ~365.25 times per year relative to
the sun to produce ~365.25 days per year. However, as measured by the
rest of the stars in the universe, our absolute number of rotations per
year is one more: 365.25 + 1.00 = 366.25.
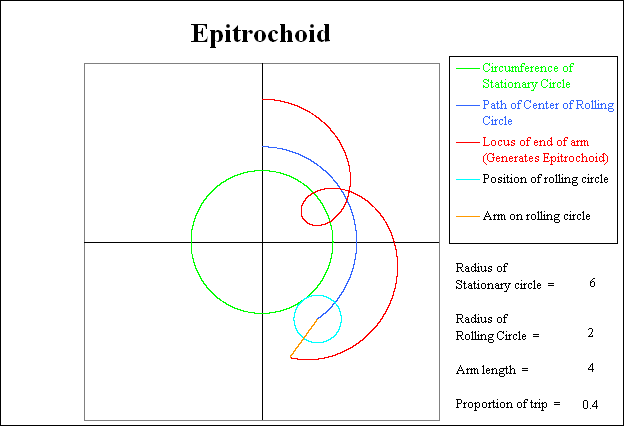
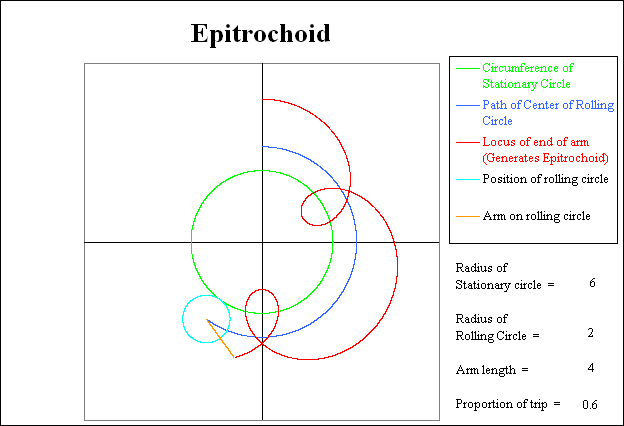
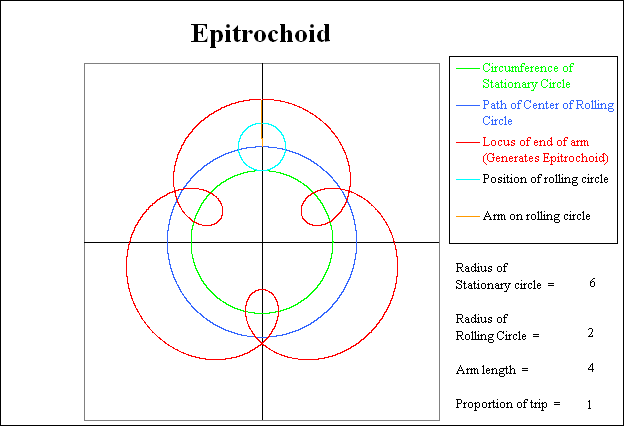
Finally after the rolling circle has completed 3
revolutions relative to the stationary circle (and completed 4
revolutions relative to the coordinate system), the rolling circle has
returned to the starting position, and the Epitrochoid is complete.
While the above example displays one of the infinite
number of possible Epitrochoids, slight changes in the dimensions that
are used can produce other interesting patterns.
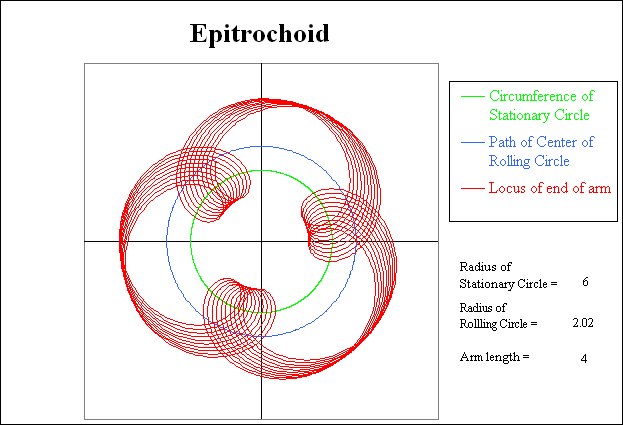
In the picture above, the radius of the rolling circle has
been increased from 2.00 to 2.02. Thus the distance required to
complete 3 rolling rotations around the stationary circle increases
slightly from 6.00 to 6.06. The diagram shows the result of 30 rolls
relative to the stationary circle. The slightly increased total
distance produces a clockwise rotational precession in the resulting
pattern.
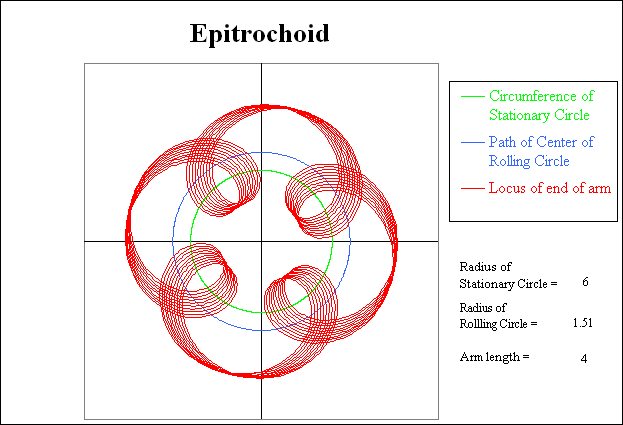
Another change in the radius of the rolling circle
produces the above pattern. If the radius had been set to exactly 1.50,
then a simple Epitrochoid with 4 loops would have resulted. However, by
setting the radius to 1.51, another precession pattern is produced.
For additional information about Epitrochoids and the
mathematics required to generate them, please see http://mathworld.wolfram.com/Epitrochoid.html
Hypotrochoids
If the circle rolls around the inside
of a stationary circle, then the result is a Hypotrochoid.
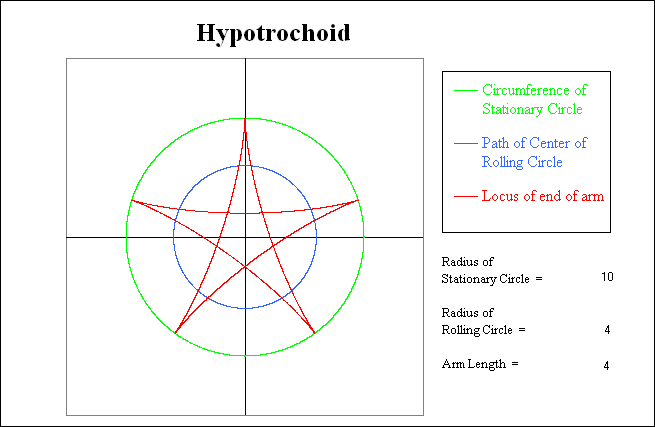
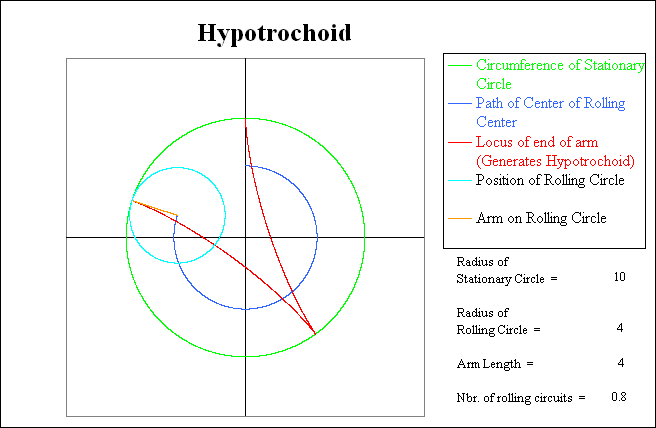
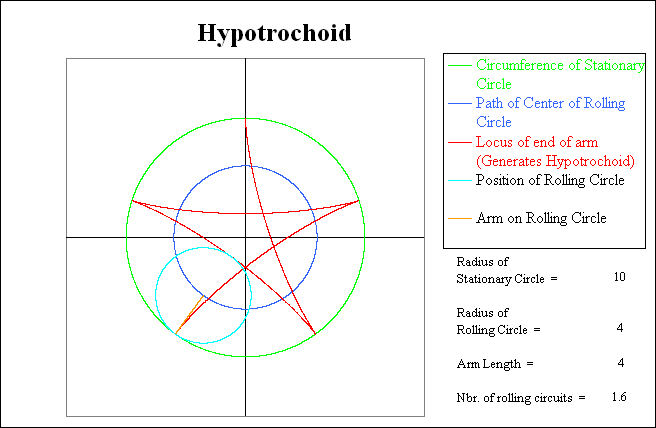
In the example shown here, the stationary circle has a
radius of 10. A circle with a radius of 4 rolls around the inside of
the stationary circle. Again, the dark blue circle traces the path of
the center of the rolling circle. The arm length is the same as the
radius of the rolling circle, and thus the end of the arm is
essentially the same as a point on the rolling circle. The red line is
a trace of this point, and it generates a Hypotrochoid en route as it
returns to its starting location. The diagrams below illustrate various
stages of this path.
The picture above shows the starting conditions. The
rolling circle is shown in light blue and the arm is again shown in
orange as it overlies part of the vertical axis.
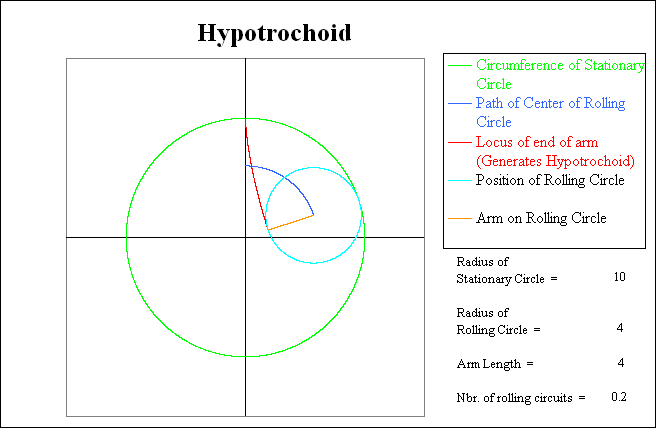
This next picture shows the interim result after the
rolling circle has completed 20 % of its first circuit around the
inside of the stationary circle. Note that while the rolling circle is
traveling clockwise, the arm on the rolling circle is rotating
counterclockwise. For each trip that the rolling circle makes around
the inside of the stationary circle, the arm will make 10 / 4 = 2.5
counterclockwise revolutions relative to the stationary circle. (Count
the number of arm contacts with the green circle.) However, since the
relative rotation of the arm is opposite to the rolling direction of
the circle, the absolute number of arm rotations as measured by the
coordinate systems is one less than this: 2.5 - 1.0 = 1.5.
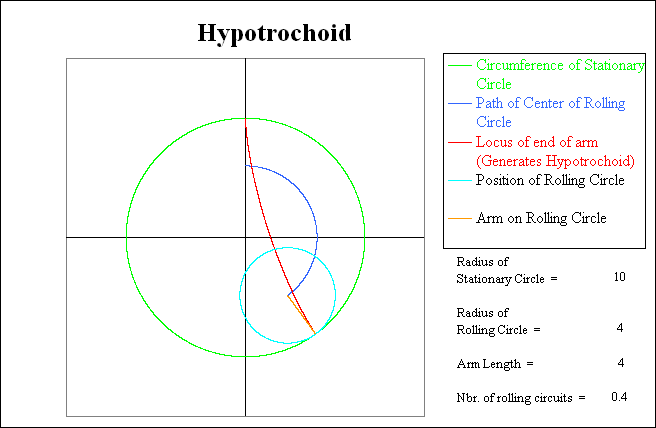
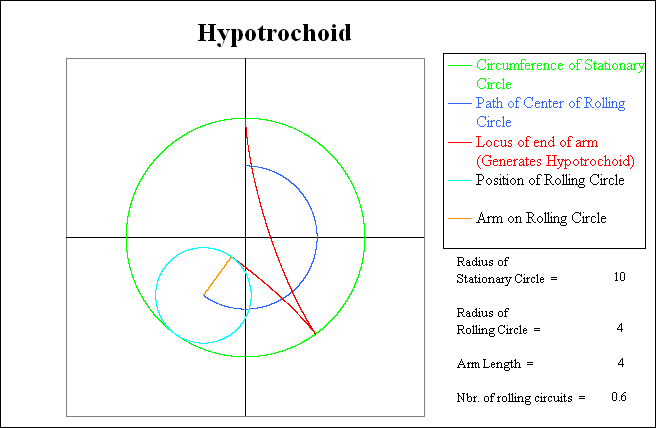
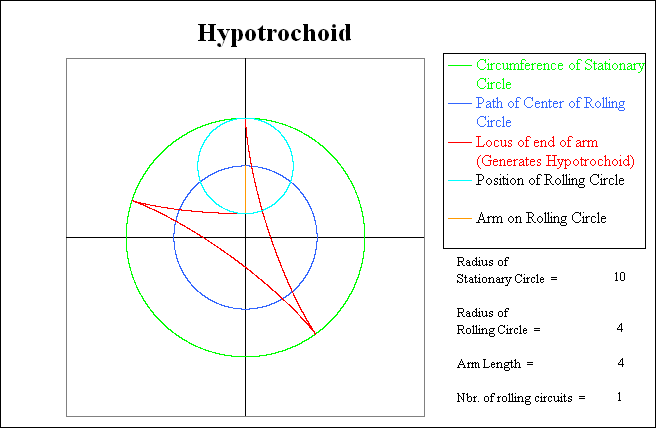
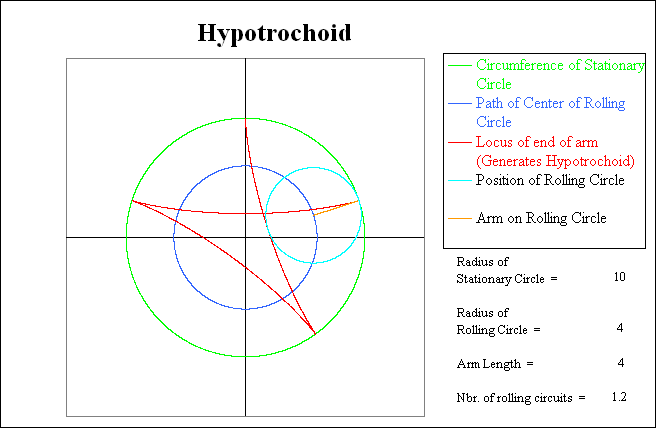
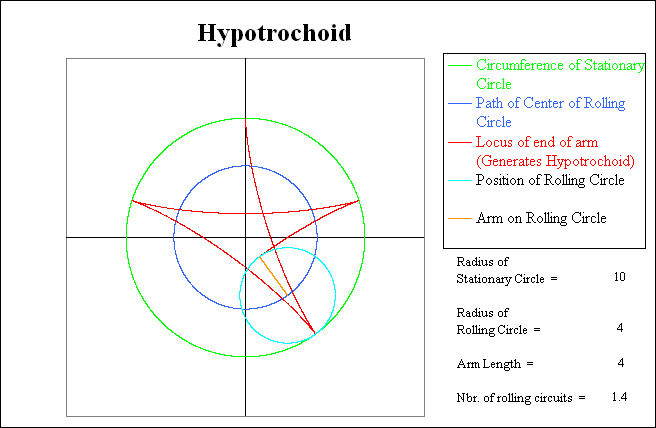
Note that when the light blue rotating circle has returned
to the starting point, the red trace shows that it has gone thru 2.5
rotations relative to the green stationary circle, but has only
completed 1.5 rotations relative to the coordinate system. At this
point the Hypotrochoid (red line) is only one-half complete, and thus
the rolling circle will have to make another circuit to complete the
pattern.
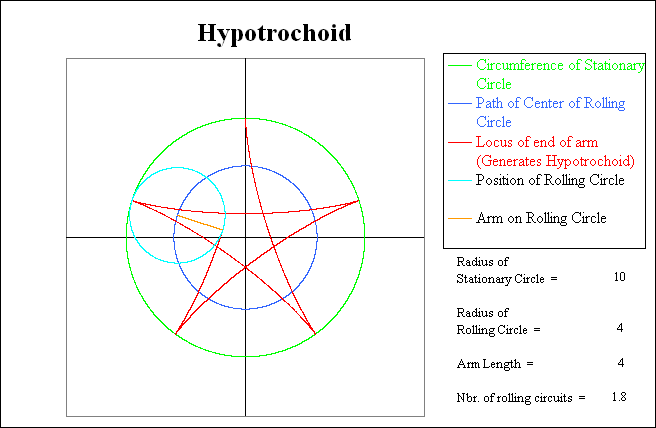
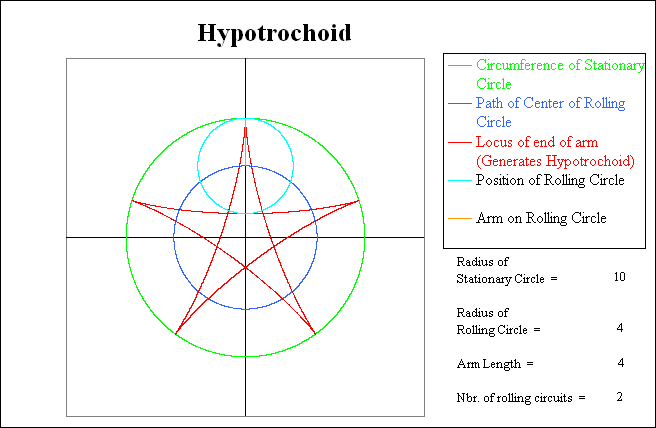
As is the case with Epitrochoids, it’s interesting
to experiment with various circle sizes to see what happens. One
interesting phenomenon occurs when you set the radius of the rolling
circle (and arm length) to 6 instead of 4. The red line traces an
identical pattern, but this time it traces it backwards. Also the
rolling circle has to make 3 circuits instead of two.
For additional information about Hypotrochoids and the
mathematics required to generate them, please see http://mathworld.wolfram.com/Hypotrochoid.html
Return to Durango Bill’s
main page
Web page generated via KompoZer
