
Durango Bill's
Enumeration of
Binary Trees
Enumeration of All Possible Binary Trees
Enumeration of Structurally Different Binary Trees
A binary tree is rooted tree where each vertex can have a maximum of two edges that connect to lower portions of the tree. (Please see the "Trees" link from the main page for a definition of generic trees.) The "root" is normally depicted at the top. Edges from any vertex in the tree will descend either to the left (left branch) or to the right (right branch).
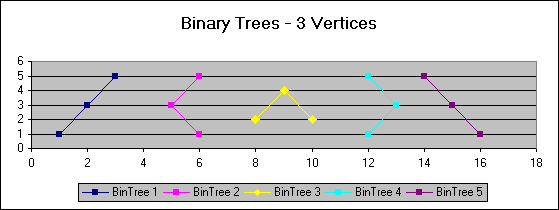
The diagram above illustrates all possible binary trees that can be created with 3 vertices. If we want to consider binary trees that are structurally different, then trees 1, 2, 4, and 5 are structurally the same. (Tree 3 is different.) Binary trees are structurally the same if combinations of mirror images (left to right flips) can convert one version of a tree into another. For example, a mirror image flip taken at the top vertex of Tree 5 will convert it into Tree 1. Also a mirror image flip taken at the middle vertex of Tree 2 (and only using that portion of the tree below this vertex) will convert it into Tree 1.
Method 1) If we know how many different binary trees exist up through "N" vertices, then we can calculate the number at "N + 1" via the following observations. We start by putting the "N + 1"th vertex at the root (top). Then we note that all binary trees that have "N" vertices could be tacked on to the left branch from this new vertex. We could add to this all binary trees that have "N - 1" vertices tacked to the left branch of the root combined with all trees that have 1 vertex tacked to the right branch. Continuing, we add to our total all binary trees that have "N - 2" vertices tacked to the left branch combined with all binary trees that have 2 vertices tacked to the right. We continue this process through "0" vertices tacked to the left branch and "N" vertex trees tacked to the right branch. If we use this algorithm to find the "Number of Binary Trees" for N = 8 we get: 429*1 + 132*1 + 42*2 + 14*5 + 5*14 + 2*42 + 1*132 + 1*429 = 1,430. (Check the above table to verify the source of these numbers.
Method 2) There is a direct equation.
Number of Binary Trees[n] = COMBIN(2n, n) / (n + 1)
This can be extended to enumerate all “t-ary” trees via:
Number of t-ary Trees[n] = COMBIN(tn + 1, n) / (tn + 1)
Method 3) First we note that the coefficients (1, 1, 2, 5, 14, 42, etc.) form a Catalan Sequence. This can be derived from a modified Pascal's Triangle of binomial coefficients.
1
1 | 1
| 1 1
1 | 2 1
| 2 3 1
2 | 5 4 1
| 5 9 5 1
5 | 14 14 6 1
| 14 28 20 7 1
14 | 42 48 27 8 1
Each number in the table is the sum of the numbers that appear to the left and right immediately above it with the following exception. At the vertical line, the upper left number does not contribute its portion. The numbers to the left of the vertical line produce the desired coefficients.
Method 4) There is a simple step for producing Catalan Numbers. This is illustrated below.
Index Catalan
Number Number
----------------
1 1
2 1
3 2
4 5
5 14
N C[N-1]*(4N-6)/N
The index is off by one but this can be easily adjusted in a computer program.
When we calculate the number of structurally different trees, we have to define a system to differentiate between different trees that have the same structure. Thus at each vertex in the tree, we will place the subtree that has the greatest number of vertices on the left branch, and put the subtree with the smaller number of vertices on the right. If both subtrees have the same number of vertices, we arbitrarily assign a letter (A, B, C, etc.) to each different subtree structure. Then we keep the letters in alphabetical order.
The "Number of Structurally Different Binary Trees" can be calculated easily using Method 1) from above. If we imagine the column on the right as the contents of an array, then A[N] equals the value of the array at position "N". For example A[9] = 98. If we want to calculate A[10] given we have all the values up to A[9], then we form products using the first half of the Method 1) algorithm above. Thus, we calculate: 98*1 + 46* 1 + 23*1 + 11*2 + 6*3 = 207. In general if "N + 1" is even, then A[N+1] = A[N]*A[0] + A[N-1]*A[1] + A[N-2]*A[2] etc. and then stop before the two references cross.
If "N+1" is an odd number, there is a slight complication, as the two references will exactly meet in the middle. Let's calculate A[11] to see the difference. The first part of the calculation is the same. We start at the two ends and work toward the middle until we get to the middle. Thus we have: 207*1 + 98*1 + 46*1 + 23*2 + 11*3 = 430. Then the two converging indexes meet at A[5] = 6.
The 6 indicates that our new "root" node will have one of the 6 structurally different subtrees attached to its left branch, and another of the 6 possible subtrees attached to the right branch. Let's designate these 6 structurally different subtrees with the letters A, B, C, D, E, and F.
If "A" goes on the left branch, then the right branch could have and A, B, C, D, E, or F for 6 combinations. If "B" goes on the left branch, then the right branch could get a B, C, D, E, or F for 5 more combinations. ("A" can't go on the right branch, as that would violate our alphabetical order). If "C" goes on the left, there are 4 more possible combinations. D, E, and F similarly produce 3, 2, and 1 more combinations. Thus if the contents of A[midpoint] is 6, then there are 6 + 5 + 4 + 3 + 2 + 1 = 21 combinations. If we add this 21 to the previous 430, we get 451 which is the correct value for A[11].
In general, if we are calculating A[N], we form the vector product down to where the two indexes are about to meet. If N is even this completes the process. If N is odd, then the two indexes will meet at a midpoint. We then take the array value at this midpoint and form the sum of all integers from here down to 1. (If the value at the midpoint is "X", then sum X + (X-1) + (X-2)...+ 1 = X(X+1)/2). Finally add this amount to the prior vector product.
Return to Durango Bill's Home Page
Web page generated via Sea Monkey's Composer
within a Linux Cinnamon Mint 18 operating system.
(Goodbye Microsoft)
Enumeration of All Possible Binary Trees
Enumeration of Structurally Different Binary Trees

A binary tree is rooted tree where each vertex can have a maximum of two edges that connect to lower portions of the tree. (Please see the "Trees" link from the main page for a definition of generic trees.) The "root" is normally depicted at the top. Edges from any vertex in the tree will descend either to the left (left branch) or to the right (right branch).
The diagram above illustrates all possible binary trees that can be created with 3 vertices. If we want to consider binary trees that are structurally different, then trees 1, 2, 4, and 5 are structurally the same. (Tree 3 is different.) Binary trees are structurally the same if combinations of mirror images (left to right flips) can convert one version of a tree into another. For example, a mirror image flip taken at the top vertex of Tree 5 will convert it into Tree 1. Also a mirror image flip taken at the middle vertex of Tree 2 (and only using that portion of the tree below this vertex) will convert it into Tree 1.

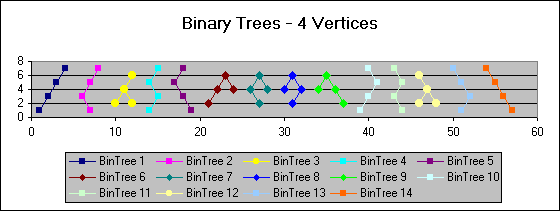
We can go one
step deeper by looking at binary trees that have 4
vertices. All 14 possible binary trees with 4 vertices are
shown above. However, there are only 3 structurally
different variations. Trees1, 2, 4, 5, 10, 11, 13, and 14
share a common structure. Trees 3 and 12 have a second
structure. Finally, trees 6, 7, 8, and 9 share a third
structure. Note that any tree within a given structure can
be converted into any other tree within the same structure
group by combinations of various "flips" (mirror images)
of the subtrees at the appropriate vertices.
At this point we
might wonder how many possible binary trees exit for any
given "N" vertices, and how many of these are structurally
different. We will give the results first and then outline
the algorithms showing how the data is calculated. (Note:
we have included a "0" vertex row as this will be used in
the calculation algorithms.)
Number
of possible binary trees and the number of structurally
different binary trees
Computer
Program by Bill Butler
Number of
Number of
Number of
Structurally
Vertices Binary Trees Different Binary Trees
--------- ------------ ----------------------
0 1 1
1 1 1
2 2 1
3 5 2
4 14 3
5 42 6
6 132 11
7 429 23
8 1,430 46
9 4,862 98
10 16,796 207
11 58,786 451
12 208,012 983
13 742,900 2,179
14 2,674,440 4,850
15 9,694,845 10,905
16 35,357,670 24,631
17 129,644,790 56,011
18 477,638,700 127,912
19 1,767,263,190 293,547
20 6,564,120,420 676,157
21 24,466,267,020 1,563,372
22 91,482,563,640 3,626,149
23 343,059,613,650 8,436,379
24 1,289,904,147,324 19,680,277
25 4,861,946,401,452 46,026,618
26 18,367,353,072,152 107,890,609
27 69,533,550,916,004 253,450,711
28 263,747,951,750,360 596,572,387
29 1,002,242,216,651,368 1,406,818,759
30 3,814,986,502,092,304 3,323,236,238
31 14,544,636,039,226,909 7,862,958,391
32 55,534,064,877,048,198 18,632,325,319
33 212,336,130,412,243,110 44,214,569,100
34 812,944,042,149,730,764 105,061,603,969
35 3,116,285,494,907,301,262 249,959,727,972
36 1.195980E+19 595,405,363,473
37 4.595080E+19 1,419,855,914,607
38 1.767339E+20 3,389,524,479,050
39 6.804254E+20 8,099,766,813,570
40 2.622127E+21 19,374,186,136,140
45 2.257118E+24 1,536,638,374,367,584
50 1.978262E+27 124,115,016,909,960,463
60 1.583851E+33 8.442062E+20
70 1.321422E+39 5.985396E+24
80 1.136360E+45 4.374817E+28
90 1.000135E+51 3.272993E+32
100 8.965199E+56 2.494155E+36
200 5.122015E+116 2.813960E+75
300 4.488636E+176 4.874205E+114
400 4.689338E+236 1.006726E+154
500 5.394975E+296 2.290014E+193
1000 2.046103E+597 2.625408E+390
2000 8.310334E+1198 9.747673E+784
3000 5.194627E+1800 5.570432E+1179
4000 3.874166E+2402 3.798171E+1574
5000 3.182944E+3004 2.852927E+1969
6000 2.780128E+3606 2.278211E+2364
7000 2.533072E+4208 1.897777E+2759
8000 2.380453E+4810 1.630521E+3154
For large N use: For large N use:
4^N/{(N)(Sqrt(PI*N))} 0.791603*2.48325^N*N^(-1.5)
Vertices Binary Trees Different Binary Trees
--------- ------------ ----------------------
0 1 1
1 1 1
2 2 1
3 5 2
4 14 3
5 42 6
6 132 11
7 429 23
8 1,430 46
9 4,862 98
10 16,796 207
11 58,786 451
12 208,012 983
13 742,900 2,179
14 2,674,440 4,850
15 9,694,845 10,905
16 35,357,670 24,631
17 129,644,790 56,011
18 477,638,700 127,912
19 1,767,263,190 293,547
20 6,564,120,420 676,157
21 24,466,267,020 1,563,372
22 91,482,563,640 3,626,149
23 343,059,613,650 8,436,379
24 1,289,904,147,324 19,680,277
25 4,861,946,401,452 46,026,618
26 18,367,353,072,152 107,890,609
27 69,533,550,916,004 253,450,711
28 263,747,951,750,360 596,572,387
29 1,002,242,216,651,368 1,406,818,759
30 3,814,986,502,092,304 3,323,236,238
31 14,544,636,039,226,909 7,862,958,391
32 55,534,064,877,048,198 18,632,325,319
33 212,336,130,412,243,110 44,214,569,100
34 812,944,042,149,730,764 105,061,603,969
35 3,116,285,494,907,301,262 249,959,727,972
36 1.195980E+19 595,405,363,473
37 4.595080E+19 1,419,855,914,607
38 1.767339E+20 3,389,524,479,050
39 6.804254E+20 8,099,766,813,570
40 2.622127E+21 19,374,186,136,140
45 2.257118E+24 1,536,638,374,367,584
50 1.978262E+27 124,115,016,909,960,463
60 1.583851E+33 8.442062E+20
70 1.321422E+39 5.985396E+24
80 1.136360E+45 4.374817E+28
90 1.000135E+51 3.272993E+32
100 8.965199E+56 2.494155E+36
200 5.122015E+116 2.813960E+75
300 4.488636E+176 4.874205E+114
400 4.689338E+236 1.006726E+154
500 5.394975E+296 2.290014E+193
1000 2.046103E+597 2.625408E+390
2000 8.310334E+1198 9.747673E+784
3000 5.194627E+1800 5.570432E+1179
4000 3.874166E+2402 3.798171E+1574
5000 3.182944E+3004 2.852927E+1969
6000 2.780128E+3606 2.278211E+2364
7000 2.533072E+4208 1.897777E+2759
8000 2.380453E+4810 1.630521E+3154
For large N use: For large N use:
4^N/{(N)(Sqrt(PI*N))} 0.791603*2.48325^N*N^(-1.5)
There are
several ways the "Number of Binary Trees" column can
be calculated.
Method 1) If we know how many different binary trees exist up through "N" vertices, then we can calculate the number at "N + 1" via the following observations. We start by putting the "N + 1"th vertex at the root (top). Then we note that all binary trees that have "N" vertices could be tacked on to the left branch from this new vertex. We could add to this all binary trees that have "N - 1" vertices tacked to the left branch of the root combined with all trees that have 1 vertex tacked to the right branch. Continuing, we add to our total all binary trees that have "N - 2" vertices tacked to the left branch combined with all binary trees that have 2 vertices tacked to the right. We continue this process through "0" vertices tacked to the left branch and "N" vertex trees tacked to the right branch. If we use this algorithm to find the "Number of Binary Trees" for N = 8 we get: 429*1 + 132*1 + 42*2 + 14*5 + 5*14 + 2*42 + 1*132 + 1*429 = 1,430. (Check the above table to verify the source of these numbers.
Method 2) There is a direct equation.
Number of Binary Trees[n] = COMBIN(2n, n) / (n + 1)
This can be extended to enumerate all “t-ary” trees via:
Number of t-ary Trees[n] = COMBIN(tn + 1, n) / (tn + 1)
Method 3) First we note that the coefficients (1, 1, 2, 5, 14, 42, etc.) form a Catalan Sequence. This can be derived from a modified Pascal's Triangle of binomial coefficients.
1
1 | 1
| 1 1
1 | 2 1
| 2 3 1
2 | 5 4 1
| 5 9 5 1
5 | 14 14 6 1
| 14 28 20 7 1
14 | 42 48 27 8 1
Each number in the table is the sum of the numbers that appear to the left and right immediately above it with the following exception. At the vertical line, the upper left number does not contribute its portion. The numbers to the left of the vertical line produce the desired coefficients.
Method 4) There is a simple step for producing Catalan Numbers. This is illustrated below.
Index Catalan
Number Number
----------------
1 1
2 1
3 2
4 5
5 14
N C[N-1]*(4N-6)/N
The index is off by one but this can be easily adjusted in a computer program.
Calculating
the
number of structurally different trees
When we calculate the number of structurally different trees, we have to define a system to differentiate between different trees that have the same structure. Thus at each vertex in the tree, we will place the subtree that has the greatest number of vertices on the left branch, and put the subtree with the smaller number of vertices on the right. If both subtrees have the same number of vertices, we arbitrarily assign a letter (A, B, C, etc.) to each different subtree structure. Then we keep the letters in alphabetical order.
The "Number of Structurally Different Binary Trees" can be calculated easily using Method 1) from above. If we imagine the column on the right as the contents of an array, then A[N] equals the value of the array at position "N". For example A[9] = 98. If we want to calculate A[10] given we have all the values up to A[9], then we form products using the first half of the Method 1) algorithm above. Thus, we calculate: 98*1 + 46* 1 + 23*1 + 11*2 + 6*3 = 207. In general if "N + 1" is even, then A[N+1] = A[N]*A[0] + A[N-1]*A[1] + A[N-2]*A[2] etc. and then stop before the two references cross.
If "N+1" is an odd number, there is a slight complication, as the two references will exactly meet in the middle. Let's calculate A[11] to see the difference. The first part of the calculation is the same. We start at the two ends and work toward the middle until we get to the middle. Thus we have: 207*1 + 98*1 + 46*1 + 23*2 + 11*3 = 430. Then the two converging indexes meet at A[5] = 6.
The 6 indicates that our new "root" node will have one of the 6 structurally different subtrees attached to its left branch, and another of the 6 possible subtrees attached to the right branch. Let's designate these 6 structurally different subtrees with the letters A, B, C, D, E, and F.
If "A" goes on the left branch, then the right branch could have and A, B, C, D, E, or F for 6 combinations. If "B" goes on the left branch, then the right branch could get a B, C, D, E, or F for 5 more combinations. ("A" can't go on the right branch, as that would violate our alphabetical order). If "C" goes on the left, there are 4 more possible combinations. D, E, and F similarly produce 3, 2, and 1 more combinations. Thus if the contents of A[midpoint] is 6, then there are 6 + 5 + 4 + 3 + 2 + 1 = 21 combinations. If we add this 21 to the previous 430, we get 451 which is the correct value for A[11].
In general, if we are calculating A[N], we form the vector product down to where the two indexes are about to meet. If N is even this completes the process. If N is odd, then the two indexes will meet at a midpoint. We then take the array value at this midpoint and form the sum of all integers from here down to 1. (If the value at the midpoint is "X", then sum X + (X-1) + (X-2)...+ 1 = X(X+1)/2). Finally add this amount to the prior vector product.
Return to Durango Bill's Home Page
Web page generated via Sea Monkey's Composer
within a Linux Cinnamon Mint 18 operating system.
(Goodbye Microsoft)